Check this post in English 🇬🇧.
Hoy no vengo a hablar de datos, sino de simulaciones y de cómo la inteligencia artificial puede ayudarnos a calcular probabilidades mediante el método de Monte Carlo.
Como ya he comentado otras veces en el blog, Twitter/X suele ser una fuente de inspiración para mí. Esta vez, fue un problema matemático que vi en este tweet.
Juego de casino
Un casino ofrece un juego de cartas con una baraja normal de 52 cartas. La regla es que se voltean dos cartas a la vez.
Si ambas cartas son negras, van al montón del crupier. Si ambas cartas son rojas, van a tu montón. Si una es negra y la otra roja, se descartan.
Este proceso se repite hasta que se hayan usado las 52 cartas. Si al final tienes más cartas en tu montón que el crupier, ganas 100 $. Si no (incluyendo empates), no ganas nada.
¿Cuánto estarías dispuesto a pagar por jugar a este juego?
Resolviendo el problema con la IA
Decidí abordar este problema con ChatGPT (Podéis ver el prompt y resultado en este tweet). La IA no solo proporcionó el código para simular el juego, sino que también me dio la solución tras ejecutarlo: no valía la pena pagar ni un solo dólar por jugar.
Una estimulante discusión con un quant me llevó a dos conclusiones:
- Que la IA no proporcionaba una respuesta correcta cuando le pedía una explicación matemática del problema.
- Que el quant se equivocó en su respuesta, y que el resultado de la IA era, en efecto, correcto: todas las simulaciones acababan en empate, así que era imposible ganar.
Las matemáticas nunca han sido mi fuerte, y quizás por eso disfruto tanto resolviendo estos problemas con el método de Monte Carlo. En mi etapa en el sector financiero, me fascinó ver cómo los quants usaban simulaciones para calcular probabilidades en todo tipo de estrategias. Así que, con este problema como excusa, quise explorar sus variables y ver cómo la IA me podía echar una mano.
¿Y Si Cambiamos un Poco las Reglas del Juego?
En el problema original, era imposible ganar: el juego siempre terminaba en empate. Pero, ¿y si cambiamos las reglas? Imaginemos que los pares de distinto color (una carta roja y una negra) vuelven al mazo en vez de descartarse. Usando Cursor, modifiqué el código para simular este nuevo escenario:
def simulate_game_with_replacement():
"""Simulation where mixed pairs are added back to the deck."""
# Create initial deck
deck = ['R'] * 26 + ['B'] * 26
random.shuffle(deck)
# Initialize counts
X = 0 # Red-red pairs
Y = 0 # Black-black pairs
# Process cards until deck is empty
while len(deck) >= 2:
# Draw a pair
card1 = deck.pop(0)
card2 = deck.pop(0)
if card1 == 'R' and card2 == 'R':
X += 1
elif card1 == 'B' and card2 == 'B':
Y += 1
else:
# Mixed pair - add cards back to the deck and shuffle
deck.extend([card1, card2])
random.shuffle(deck)
El resultado fue este:
Probability of winning (X > Y): 0.000
Probability of losing (X < Y): 0.000
Probability of tying (X = Y): 1.000
Expected value: $0.00
¡Nada! Esta variante también acababa en empate, así que seguíamos sin poder ganar. Pero, ¿y si complicamos un poco más las cosas? ¿Qué pasaría si quitamos la primera carta del mazo, jugamos la partida (descartando los pares de distinto color como antes) y, además, descartamos la última carta que quede en el mazo?
Solo necesité modificar un par de líneas de código:
# Discard one card before starting
deck.pop(0)
# Process cards until only one card is left
while len(deck) > 1:
El resultado fue este:
Probability of winning (X > Y): 0.245
Probability of losing (X < Y): 0.245
Probability of tying (X = Y): 0.510
Expected value: $24.51
Parece que con esta variante sí que podríamos llevarnos algo de dinero. La pregunta ahora es: ¿cuánto estarías dispuesto a pagar por jugar? Si pagas unos 24,50 $ (la “apuesta justa” o fair bet), a la larga, ni ganarías ni perderías dinero. Para tener opciones de ganarle al casino, tendrías que pagar menos. Si pagas más (lo que suele ocurrir), acabarías perdiendo dinero con el tiempo.
Para hacerlo más interesante, supongamos que el casino fija un precio de 20 $ y has detectado que la apuesta te favorece. Tienes 200 $ en la cartera para apostar. ¿Cuánto dinero esperarías tener después de 1000 partidas? Con la ayuda de la IA y un poco de vibe coding, generé estas imágenes:
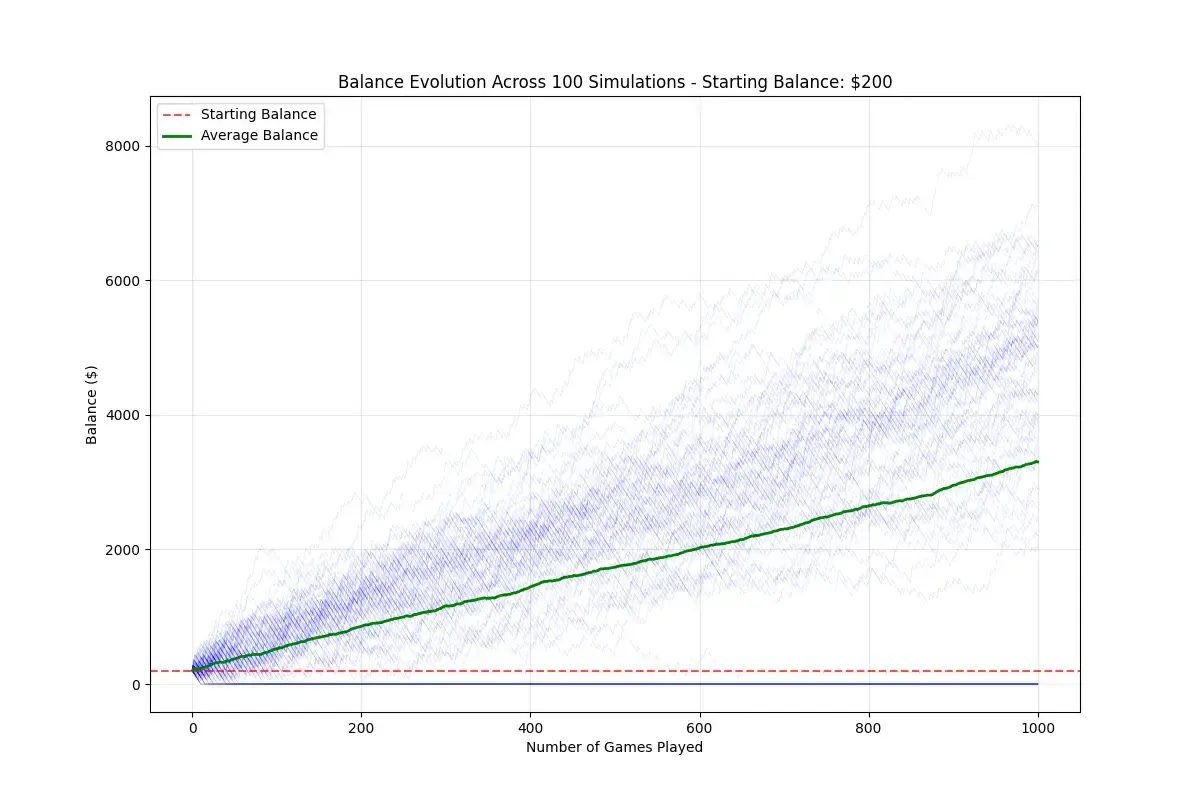
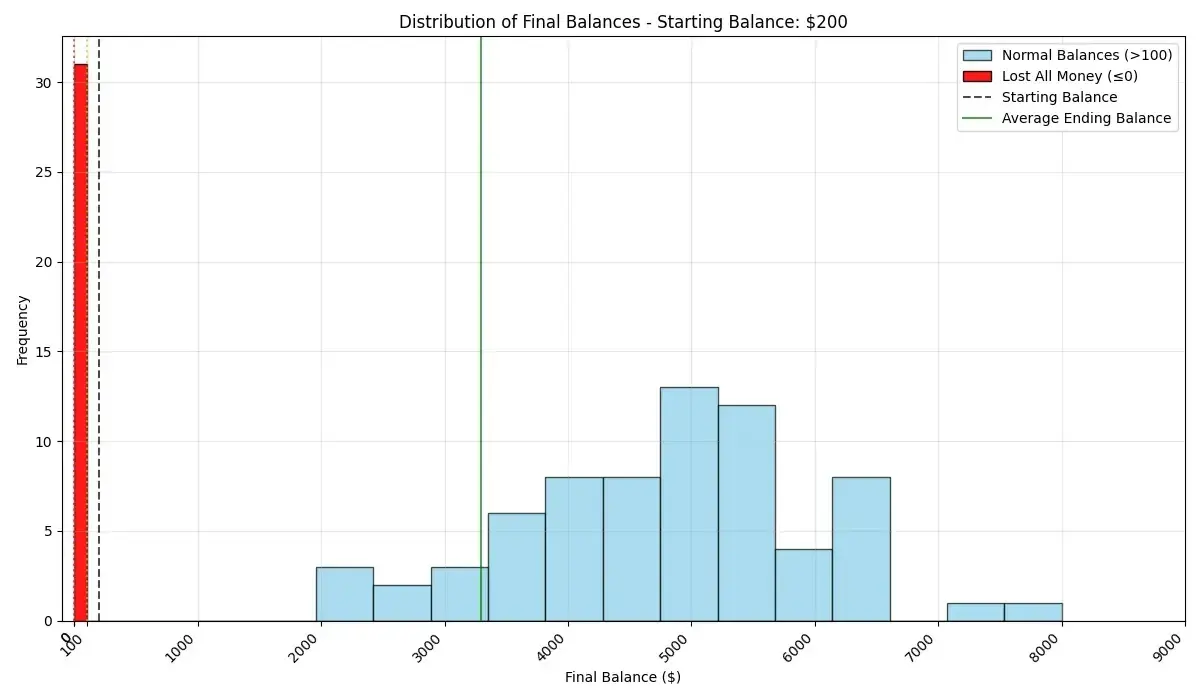
Estas simulaciones revelan algo interesante: de las 100 realizadas, en algo más de 30 perdimos todo el dinero. ¡Vaya! No es oro todo lo que reluce. Incluso sabiendo que la ventaja está de nuestro lado, si empezamos con 200 $, perderemos todo el capital aproximadamente el 30 % de las veces.
Estrategia y Gestión de Banca
En este punto, con la sensación de estar cayendo en un rabbit hole, quise plantear una última pregunta: ¿con qué cantidad de dinero debería empezar para tener un 95 % de probabilidades de no perderlo todo tras 1000 partidas?
Tras varias iteraciones con Cursor, obtuve estos resultados:
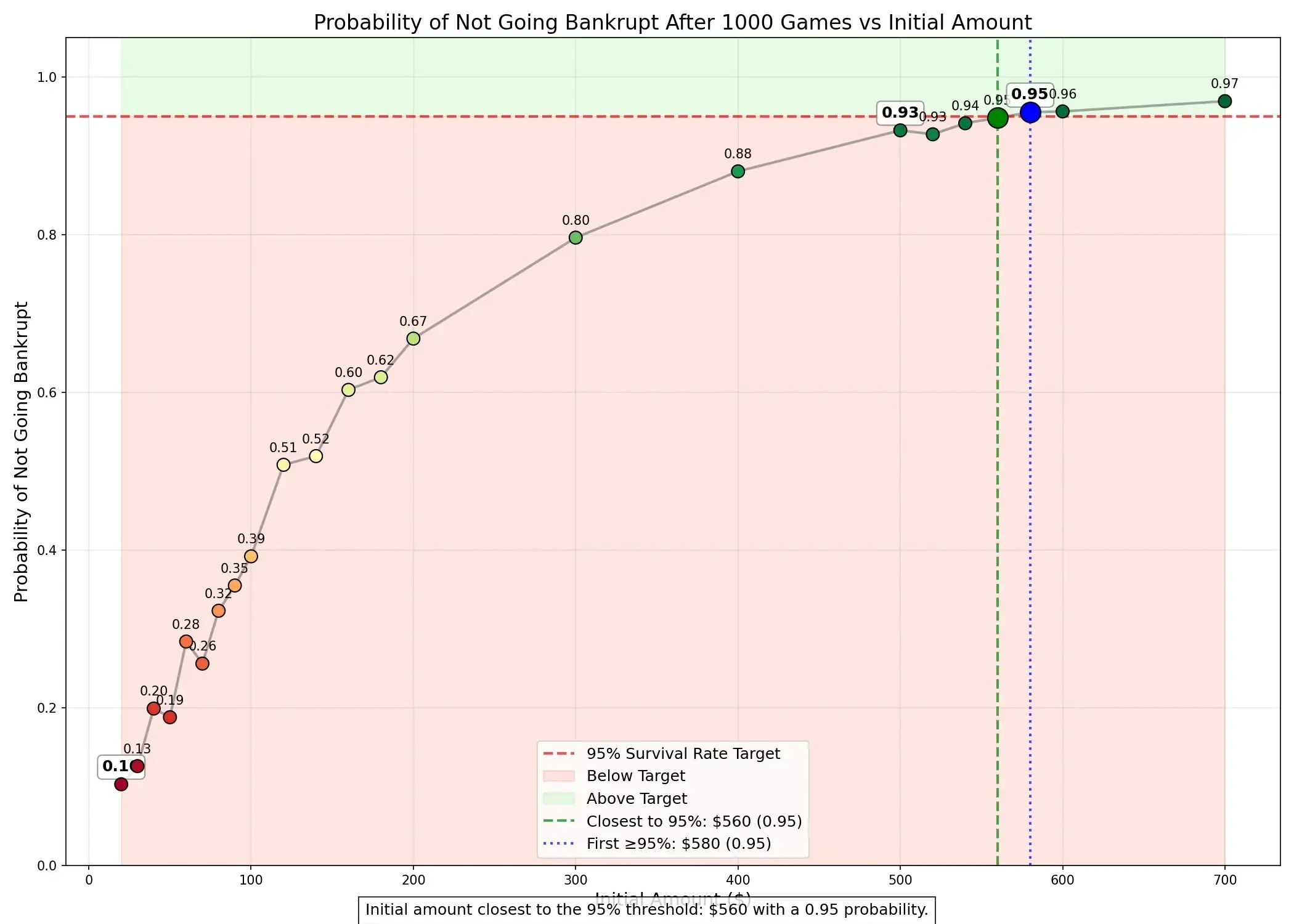
La simulación me dio la respuesta: para tener un 95 % de probabilidad de conservar el capital después de 1000 partidas, necesitaba empezar con 560 $.
Repetí la simulación del balance con esta nueva cantidad, y los resultados fueron más alentadores:
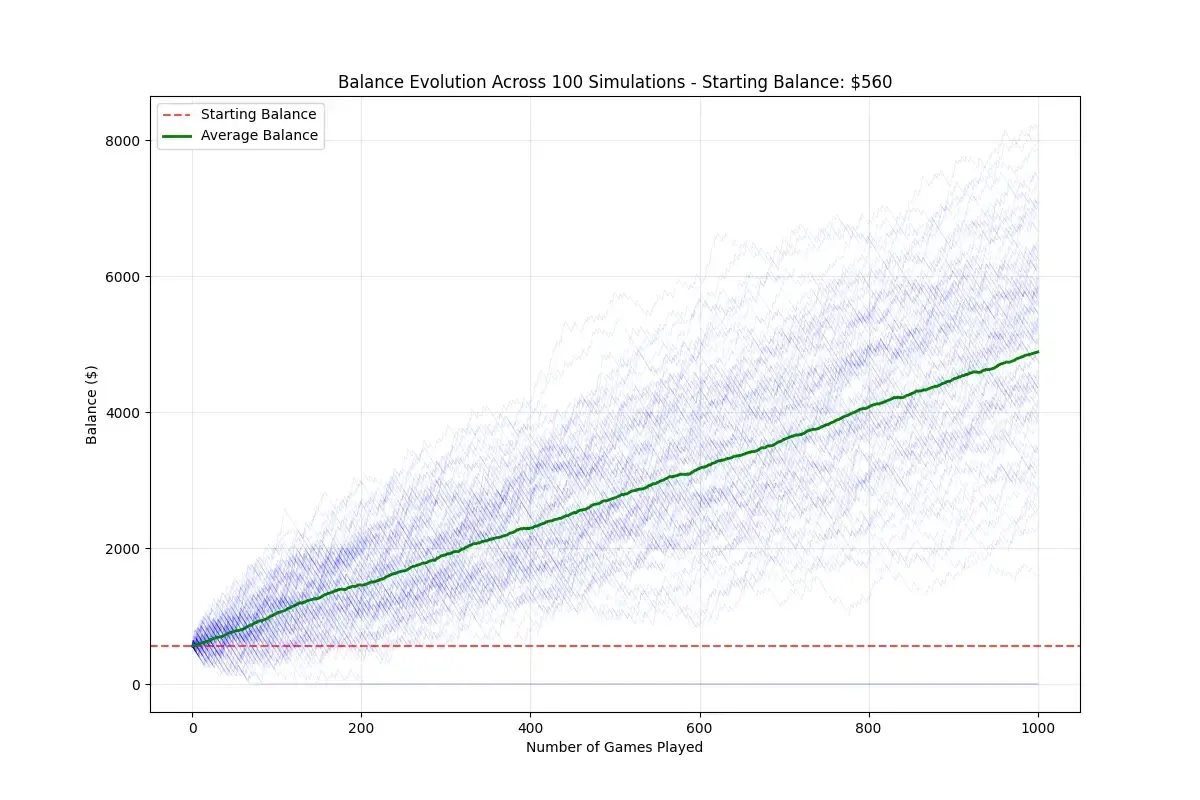
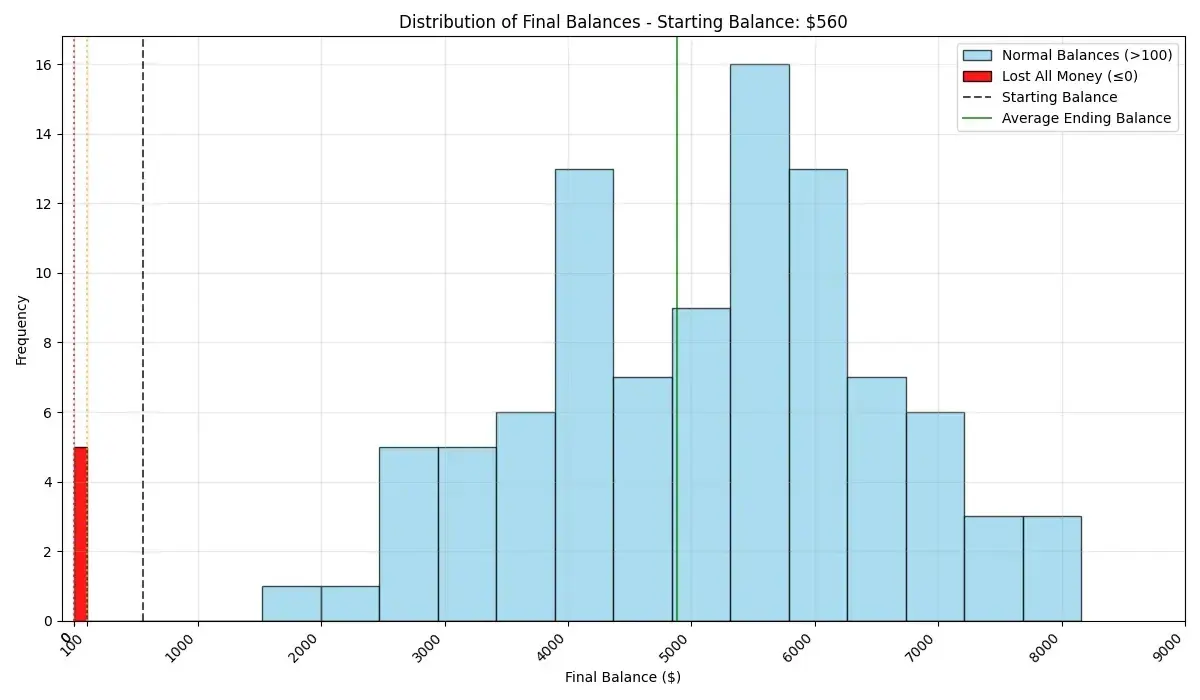
En este escenario, la ganancia esperada rondaba los 5000 $ después de 1000 partidas, con un riesgo del 5 % de perderlo todo. No suena nada mal, ¿verdad?
Reflexiones Finales
Este problema es sencillo y mi único objetivo era saciar la curiosidad. No obstante, estamos presenciando avances vertiginosos en el desarrollo de agentes capaces de idear nuevos algoritmos para problemas matemáticos complejos.
Mi reflexión es que, si bien la IA quizás aún no resuelva problemas matemáticos complejos de forma analítica, es una herramienta formidable generando código. Y esto, a su vez, le permite desarrollar algoritmos o simulaciones para abordar dichos problemas. Ahí es donde, por ahora, creo que radica gran parte de su valor: en darnos el código necesario para simular y analizar estos problemas. Estoy convencido de que el futuro traerá avances muy interesantes al combinar estas dos facetas —razonamiento matemático y computación—, que se complementarán mutuamente.